一、直方图：色彩的断层扫描

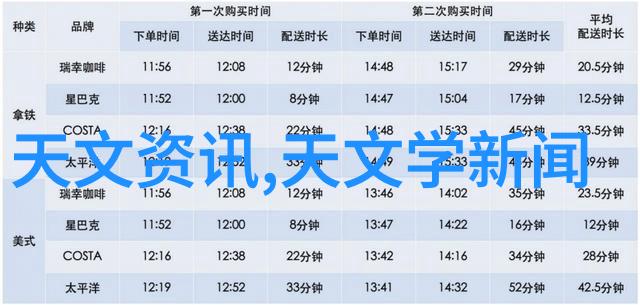
二、统计之光：直方图的计算机时代诞生

在信息爆炸的今天，数据是我们生活和工作中不可或缺的一部分。为了有效地管理和分析这些数据，我们需要一种工具来帮助我们了解它们的分布情况。这便是直方图，它是一种非常有用的可视化技术，用以展示一个连续变量的大致分布情况。它通过将数值分散成一系列的小区间，然后对每个区间内出现的数据数量进行计数，最后用柱状图表示，从而使得复杂的数字世界变得清晰易懂。

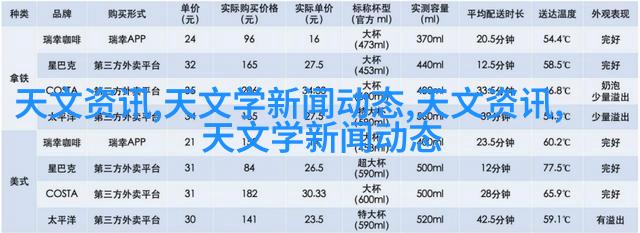
三、艺术中的数学：直方图绘制艺术探索

直方图不仅仅局限于科学领域，它同样在艺术界扮演着重要角色。在音乐和音频处理中，使用颜色编码来显示音频信号强度时，便会应用到直方图上。这样的绘制方式能够让人快速识别出音频文件中的主要特征，比如噪声水平或动态范围，这对于音乐制作师来说至关重要。

四、历史上的反思：从统计到心理学

20世纪初期，一位名叫卡尔·皮尔森（Karl Pearson）的英国统计学家，他利用了最小二乘法对各类数据进行处理，并将这种方法称为“皮尔逊积分”，这实际上就是现代意义上的累积密度函数（CDF）。这一理论后来被广泛应用于心理学领域，以此来研究人类行为模式，如情感反应与性格特征等，从而为心理学提供了一种新的观察窗口。

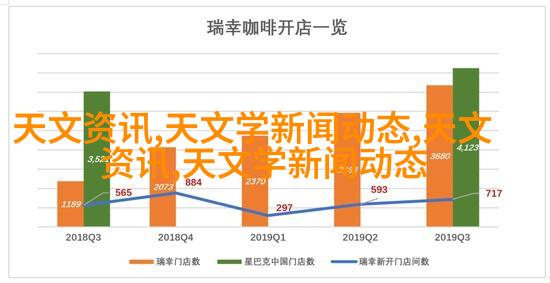
五、未来展望：人工智能与自适应算法

随着人工智能技术不断进步，我们可以期待更先进的人工神经网络模型能更好地理解并解释大量复杂数据集。而这些模型往往依赖于高效且准确的人工智能算法，其中就包括基于深度学习结构设计的一些自适应算法。这意味着未来的计算机系统可能会更加主动地调整自己的参数，以优化其处理大规模数据集所需时间，同时保持较低误差率，这正是在当前研究方向上的一大挑战，也是下一步发展的一个巨大潜力市场。